Sums of Discrete Random Variables as Banded Matrix Products
Further to the previous attempt at Fast Enumeration of Sums of Discrete Random Variables, in this new attempt we see the computation as a banded matrix-vector product with an unorthodox (and unsupported) stride of zero, and implement a custom CUDA kernel through several steps of optimization. Timings at the end. Code is available to reproduce the results.
- Recap of the problem
- Discrete enumeration as banded matrix multiplication
- Programmatic representations of banded matrices
- Custom CUDA kernels
- Results
- Further work
Recap of the problem
The basic problem is as follows:
- given a random variable on the integers with a vector of probabilities with , and
- another random variable on the integers with a vector of probabilities with ,
- consider the sum on the integers and compute its vector of probabilities with .
The basic computation is the convolution:
Discrete enumeration as banded matrix multiplication
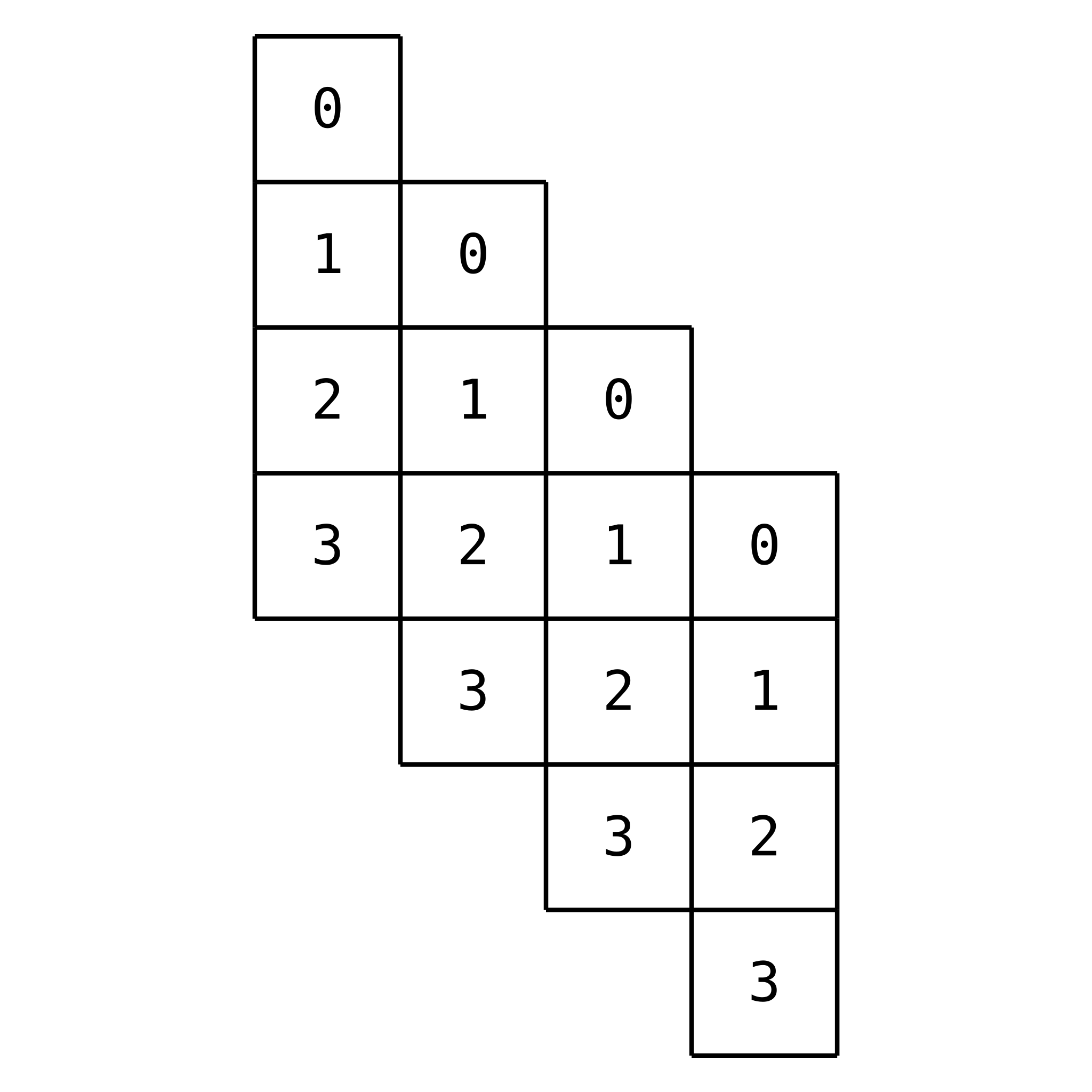
We can write this as the product of a banded matrix and a vector. Let be a function that constructs a banded matrix from a vector of length and number of columns like so:
This is a little like we might use to construct a diagonal matrix of size with all diagonal elements set to . With this function we can write the required computation in matrix form as:
We may be interested in gradients of this operation with respect to a scalar function , specifically and . Given the upstream gradient , first apply the rule for matrix multiplication (see Matrix Gradients of Scalar Functions):
Now, having , we can obtain from the mechanical construction of from :
where is the Kronecker delta (i.e. where and zero elsewhere). We can recognize this as corresponding to the matrix form:
Notice that both gradients are banded matrix-vector products too, albeit with a transpose in the mix. To summarize, we have three functions to implement:
Programmatic representations of banded matrices
Linear algebra libraries often provide support for banded matrices. BLAS provides the gbmv function family, as in cuBLAS. Unfortunately there is a catch and they cannot be used here!
A matrix in column-major order is represented in BLAS by giving a base pointer to the first element in memory (e.g. A), and a stride or lead between rows (e.g. ldA). The element in the ith row and jth column is then A[i + j*ldA]. A banded matrix in column-major order is represented by storing only the non-zero elements, and additionally providing the number of nonzero lower (e.g. kl) and upper (e.g. ku) subdiagonals. The notation , with of length , corresponds to A = x, ldA = 0, kl = m - 1, and ku = 0.
The catch? The BLAS interface requires that ldA >= max(1, m), and so we cannot use ldA = 0. It will produce an error.
We will need a custom kernel!
BLAS with arbitrary strides?
If BLAS could support arbitrary strides, we could simply use the
gbmvfamily of functions here. It would also enable other tricks that involve repeating elements, such as a base pointer to an allocation with a single element, with the stride set to zero, to represent a vector with a repeating element of any length. The challenge would be for BLAS kernels to recognize and optimize for these cases of repeated elements. Even more of a challenge would be gradients of such functions, as repeated elements in a forward pass involve reductions during a backward pass.
Eigen supports arbitrary strides
Eigen supports arbitrary strides, including zero and negative, but not banded matrices. A workaround is to break the banded matrix into lower triangular (top) and upper triangular (bottom) sections and perform the multiplication block-wise.
Custom CUDA kernels
Version 0: Starting out
For illustration, draw out the product for and . The length of will be .
The numbers are not representing the values of the elements here, but rather the associated and . We can see that the dot product of each row of the matrix with the vector is a summation of the probabilities of all pairs of and that add to the same outcome. The operation is commutative, so we will assume without loss of generality that (we can swap the order of arguments if this is not the case). This minimizes the inner dimension of the matrix multiplication.
As a first attempt, we can assign one thread to compute each element of , so threads in total:
__global__ void kernel_convolve_v0(const int m, const int n, const float* p,
const int incp, const float* q, const int incq, float* r,
const int incr) {
/* element of r for which thread is responsible */
int i = threadIdx.x + blockIdx.x*blockDim.x;
if (i < m + n - 1) {
float result = 0.0f;
for (int j = 0; j < n; ++j) {
if (0 <= i - j && i - j < m) {
result += p[(i - j)*incp]*q[j*incq];
}
}
r[i] = result;
}
}
This is a perfectly fine first attempt. However, it leaves threads with different amounts of work, according to how many times the if statement within the for loop rings true. For thread 0 it is true only once, while for thread 3 it is true four times. These numbers correspond to the number of nonzero multiplications that must be performed to compute each element of via the banded matrix-vector multiplication.
This is a form of warp divergence to be avoided if possible.
Version 1: Equalizing workload per thread
Consider the following transformation of the problem:
We now reduce from to just threads, but now threads compute two elements of instead of just one. This leaves all threads with the same number of multiplications to do.
__global__ void kernel_convolve_v1(const int m, const int n, const float* p,
const int incp, const float* q, const int incq, float* r,
const int incr) {
/* element of r for which thread is responsible */
int i = threadIdx.x + blockIdx.x*blockDim.x;
if (i < m) {
float result1 = 0.0f, result2 = 0.0f;
for (int j = 0; j < n; ++j) {
if (0 <= i - j) {
result1 += p[(i - j)*incp]*q[j*incq];
} else {
result2 += p[(m + i - j)*incp]*q[j*incq];
}
}
r[i] = result1;
if (i < n - 1) {
r[i + m] = result2;
}
}
}
Relationship to the previous attempt
This kernel is very similar to the previous attempt; the banded matrix merely offers a different perspective on the same computation. An assignment of threads, either one- or two-dimensional, gives:
The indexing is the same as before. In the one-dimensional case, thread maps to element with:
Alternatively, with two-dimensional thread indices, thread , with and , maps to element , with:
However, in the previous approach, multiple threads contributed to each output element, necessitating coordination of threads to aggregate results using atomic operations. Here we have only one thread computing each output element, meaning fewer threads and reduced parallelism, but no need for coordination.
Version 2: Using shared memory
Each thread reads all of q from device memory. We can use shared memory to read in q only once per thread block, so that all threads in the block can share the read. Doing so requires some careful use of __syncthreads() to ensure that reads and writes to shared memory are appropriately sequenced between threads. All threads must encounter the __syncthreads() calls, so the large if (i < m) { ... } is broken into finer grain controls.
__global__ void kernel_convolve_v2(const int m, const int n, const float* p,
const int incp, const float* q, const int incq, float* r,
const int incr) {
extern __shared__ float q_shared[];
/* element of r for which thread is responsible */
int i = threadIdx.x + blockIdx.x*blockDim.x;
float result1 = 0.0f, result2 = 0.0f;
for (int base_j = 0; base_j < n; base_j += blockDim.x) {
int j = threadIdx.x;
__syncthreads();
q_shared[j] = (base_j + j < n) ? q[(base_j + j)*incq] : 0.0f;
__syncthreads();
for (j = 0; j < blockDim.x; ++j) {
if (0 <= i - base_j - j) {
result1 += p[(i - base_j - j)*incp]*q_shared[j];
} else {
result2 += p[(m + i - base_j - j)*incp]*q_shared[j];
}
}
}
if (i < m) {
r[i] = result1;
if (i < n - 1) {
r[i + m] = result2;
}
}
}
Version 3: Using more shared memory
We can go further and use shared memory for the read of p too. The read pattern here is more complicated. We use the modulo operator (%) so as to never read outside the range of p, but rely on multiplying by 0.0f when outside the range of q to ensure correctness.
__global__ void kernel_convolve_v3(const int m, const int n, const float* p,
const int incp, const float* q, const int incq, float* r,
const int incr) {
extern __shared__ float shared[];
float* q_shared = shared;
float* p_shared = q_shared + 2*blockDim.x; // permits -ve indices
int i = threadIdx.x;
int j = threadIdx.x;
float result1 = 0.0f, result2 = 0.0f;
for (int base_i = blockIdx.x*blockDim.x, base_j = 0; base_j < n;
base_i -= blockDim.x, base_j += blockDim.x) {
__syncthreads();
q_shared[j] = (base_j + j < n) ? q[(base_j + j)*incq] : 0.0f;
p_shared[i] = p[((base_i + i + m) % m)*incp];
p_shared[i - blockDim.x] = p[((base_i + i - blockDim.x + m) % m)*incp];
__syncthreads();
for (int k = 0; k < blockDim.x; ++k) {
if (0 <= base_i + i - k) {
result1 += p_shared[i - k]*q_shared[k];
} else {
result2 += p_shared[i - k]*q_shared[k];
}
}
}
/* element of r for which thread is responsible */
i = threadIdx.x + blockIdx.x*blockDim.x;
if (i < m) {
r[i] = result1;
if (i < n - 1) {
r[i + m] = result2;
}
}
}
Version 4: Increasing parallelism
As it stands, the kernel offers -way parallelism by assigning one or two elements to each thread. In many cases will be insufficient to occupy the device. We can scale this up by assigning those one or two elements to a whole warp of 32 threads instead, giving -way parallelism. In doing so, however, we must also handle 32 times fewer output elements per thread block, and so reduce the benefits of the previous shared memory optimizations (by reducing the number of output elements that share each read).
It is likely that this version of the kernel will only offer improvements at small problem sizes for which the other versions do not occupy the whole GPU.
The kernel makes use of warp shuffle functions to aggregate the partial sum computed by each thread in a warp to a total sum across the warp.
__global__ void kernel_convolve_v4(const int m, const int n, const float* p,
const int incp, const float* q, const int incq, float* r,
const int incr) {
assert(blockDim.x == warpSize && gridDim.x == 1);
extern __shared__ float shared[];
float* q_shared = shared;
float* p_shared = q_shared + 2*warpSize*blockDim.y; // permits -ve indices
int i = threadIdx.y*warpSize + threadIdx.x;
int j = threadIdx.y*warpSize + threadIdx.x;
int l = threadIdx.y;
float result1 = 0.0f, result2 = 0.0f;
for (int base_i = blockIdx.y*blockDim.y, base_j = 0; base_j < n;
base_i -= warpSize*blockDim.y, base_j += warpSize*blockDim.y) {
__syncthreads();
q_shared[j] = (base_j + j < n) ? q[(base_j + j)*incq] : 0.0f;
p_shared[i] = p[((base_i + i + m) % m)*incp];
p_shared[i - warpSize*blockDim.y] = p[((base_i + i - warpSize*blockDim.y + m) % m)*incp];
__syncthreads();
for (int k = threadIdx.x; k < warpSize*blockDim.y; k += warpSize) {
if (0 <= base_i + l - k) {
result1 += p_shared[l - k]*q_shared[k];
} else {
result2 += p_shared[l - k]*q_shared[k];
}
}
}
/* sum across threads of warp, using butterfly sum */
for (int k = 16; k >= 1; k /= 2) {
result1 += __shfl_xor_sync(0xffffffff, result1, k, warpSize);
result2 += __shfl_xor_sync(0xffffffff, result2, k, warpSize);
}
/* element of r for which warp is responsible */
i = threadIdx.y + blockIdx.y*blockDim.y;
/* first thread in each warp sets the final result */
if (i < m && threadIdx.x == 0) {
r[i] = result1;
if (i < n - 1) {
r[i + m] = result2;
}
}
}
Launching the kernels
When launching to kernels we enforce that by swapping the order of the arguments if necessary. For example, a function to call version 3 might look like:
void convolve_v3(const int m, const int n, const float* p, const int incp,
const float* q, const int incq, float* r, const int incr) {
const float *p1 = p, *q1 = q;
int incp1 = incp, incq1 = incq;
int m1 = m, n1 = n;
if (n > m) {
/* swap to put largest vector on the left */
p1 = q;
q1 = p;
incp1 = incq;
incq1 = incp;
m1 = n;
n1 = m;
}
dim3 block(BLOCK_SIZE);
dim3 grid((m1 + block.x - 1)/block.x);
size_t shared = 3*block.x*sizeof(float);
kernel_convolve_v3<<<grid,block,shared>>>(m1, n1, p1, incp1, q1, incq1, r, incr);
}
Gradient kernels
Recall that the gradients require a banded matrix-vector product where the matrix is transposed. The implementation is similar to the above kernels and left as an exercise.
Results
We run the kernels on an Nvidia RTX4000 on Paperspace. Timings for each kernel version are provided in microseconds (μs), averaged over 100 repetitions, at problem sizes of and . Lower is better (faster).
| Kernel | Description | μs@65536 | μs@2048 |
|---|---|---|---|
| Version 0 | Starting out | 21041 | 122 |
| Version 1 | Equalizing workload per thread | 16317 | 133 |
| Version 2 | Using shared memory | 12987 | 130 |
| Version 3 | Using more shared memory | 7274 | 50 |
| Version 4 | Increasing parallelism | 11842 | 27 |
We see that for the larger problem size (65536), version 3 provides the best performance, while for the smaller problem size (2048), version 4 provides the best performance. This is as expected. Version 3 maximizes use of shared memory and so outperforms prior versions. Version 4 further increases parallelism, but must reduce the sharing of reads to do so. This tradeoff in version 4 is worthwhile at small problem sizes where version 3 does not occupy the GPU, but is not worthwhile at larger problem sizes where it does occupy the GPU.
Further work
Can pipeline primitives improve the shared memory kernels further?