blog

Fast Enumeration of Sums of Discrete Random Variables

A CUDA kernel.

5 min read / 22 Feb 23

I’ve been working on an upgrade to the delayed sampling implementation in Birch to remove reference cycles and reduce garbage collector overhead. One culprit for these is the handling of enumeration of sums of discrete random variables. I’ve taken the opportunity to also revisit performance, which we explore here.

The basic question:

given a random variable $x$ on the integers $\{0,\ldots,m-1\}$ with a vector of probabilities $\mathbf{p}$ with $p_i = P(x = i)$ , and
another random variable $y$ on the integers $\{0,\ldots,n-1\}$ with a vector of probabilities $\mathbf{q}$ with $q_i = P(y = i)$ ,
consider the sum $x + y$ on the integers $\{0, m + n - 2\}$ and compute its vector of probabilities $\mathbf{r}$ with $r_i = P(x + y = i)$ .

The basic computation is the convolution:

r_i = \sum_{j = \max(0,i-n+1)}^{\min (m-1,i)} p_j q_{i-j},

but the aim is to develop a kernel to compute this efficiently on GPU.

Consider the outer product $\mathbf{R} = \mathbf{p}\mathbf{q}^\top$ . To obtain $r_i$ we must sum over the $i$ th skew diagonal of $\mathbf{R}$ . To see this, assume $x$ and $y$ are on $\{0, 1, 2, 3\}$ , and consider a diagram of $\mathbf{R}$ (skewed a little): Diagram

On the left are the possible outcomes for $x$ and $y$ . Each cell corresponds to a pair of such outcomes, marked with the sum $x + y$ in the diagram, but having the probability of that pair of outcomes, $R_{xy} = p_x q_y$ , in actual fact. Pairs that yield the same sum collect along the same skew diagonal—horizontal in this orientation. Summing along those skew diagonals give the probabilities $r_{x+y}$ on the right.

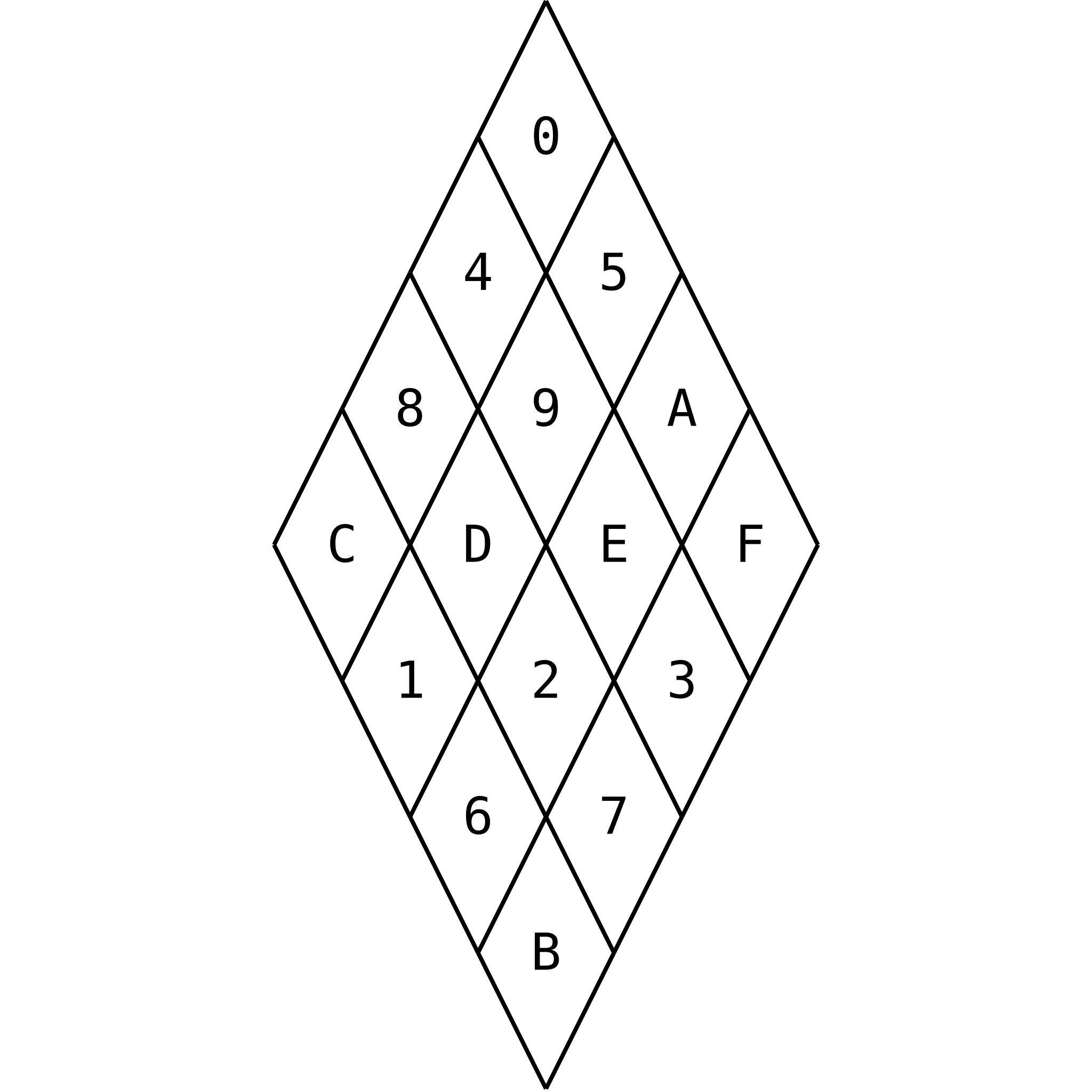
To perform those sums on GPU, we ideally make use of fast warp shuffle functions. This requires threads to be arranged by skew diagonal, not by rows and columns as is more typical. Assume a warp size of four threads (for the sake of demonstration only—it’s actually 32 threads). With the $4 \times 4$ matrix here we use 16 threads arranged into four such warps. In hexadecimal notation (i.e. $A$ through $F$ denote the decimal numbers 10 through 15), the four warps contain the threads $(0,1,2,3)$ , $(4,5,6,7)$ , $(8,9,A,B)$ and $(C,D,E,F)$ . They are assigned to elements of the matrix as follows: Diagram With this arrangement, each warp spans two skew diagonals, with the exception of the last, which has only the main skew diagonal. For example, the first warp has thread 0 on the first skew diagonal, with the single pair where $x + y = 0$ , and threads 1, 2, 3 on the fifth skew diagonal, having the three pairs where $x + y = 4$ . This ordering has a regular pattern; thread $k$ maps to element $(x,y)$ with:

\begin{aligned} x &= (\lfloor k/4 \rfloor - (k \bmod 4)) \bmod 4 \\ y &= k \bmod 4. \end{aligned}

Alternatively, with two-dimensional thread indices, thread $(i,j)$ , with $i = \lfloor k/4 \rfloor$ and $j = k \bmod 4$ , maps to element $(x,y)$ , with:

\begin{aligned} x &= (j - i) \bmod 4 \\ y &= j. \end{aligned}

We also designate a single representative thread for each skew diagonal for operations that are performed only once per unique value of $x + y$ . These are the threads for which $x \bmod 4 = 0$ or $x \bmod 4 = 3$ , excluding thread $F$ .

The above all holds for a standard warp size of 32. Just replace 4 with 32 and 3 with 31.

For $m = n = 32$ , the computation proceeds as follows:

Initialize $\mathbf{r}$ to all zero.
Launch a kernel with a two-dimensional execution configuration, of size 32 by 32.
Each thread $(i,j)$ computes $R_{ij} = p_i q_j$ and stores the result in shared memory.
All threads synchronize.
Each thread $(i,j)$ adds $R_{xy}$ to $r_{x+y}$ .

The matrix $\mathbf{R}$ is temporarily constructed in fast shared memory; no device memory is required. We can readily extend the kernel to cases where $m$ and $n$ are not 32. Larger matrices can be decomposed into tiles of size 32 by 32. Matrices where the number of rows or columns is not a multiple of 32 can be padded with zeros.

The last step can make use of warp shuffle functions, indeed this is the intention of the design. Specifically, we can use __shfl_xor_sync as in the butterfly sum example of the CUDA Programming Guide. While there is a __reduce_add_sync warp reduce function that would seem useful instead, it does not support floating point types.

A sketch of the code (untested) is as follows:

/**
 * Compute the probability distribution for a sum of two discrete random
 * variables.
 *
 * @param m Number of values for the first random variable.
 * @param n Number of values for the second random variable.
 * @param p Array of length @p m of probabilities for each value of the first
 * random variable.
 * @param incp Stride between elements of @p p.
 * @param q Array of length @p n of probabilities for each value of the
 * second random variable.
 * @param incq Stride between elements of @p q.
 * @param[out] r Array of length `m + n - 1` of probabilities for each sum.
 * @param incr Stride between elements of @p r.
 */
__global__ void kernel_add_enumerate(const int m, const int n,
    const float* p, const int incp, const float* q, const int incq, float* r,
    const int incr) {
  assert(blockDim.x == warpSize);
  assert(blockDim.y == warpSize);

  /* populate outer product */
  int x = threadIdx.x + blockIdx.x*warpSize;
  int y = threadIdx.y + blockIdx.y*warpSize;

  __shared__ R[warpSize*warpSize];
  R[threadIdx.x + threadIdx.y*warpSize] = (x < m && y < n) ? p[x]*q[y] : 0.0f;
  __syncthreads();
  
  /* local sum */
  x = (threadIdx.x - threadIdx.y) % warpSize;
  y = threadIdx.y;

  unsigned mask = 0xffffffff;
  if (x + y < warpSize) {
    mask <<= warpSize - x - y - 1;
  } else {
    mask >>= x + y + 1 - warpSize;
  }

  float value = R[x + y*warpSize];  
  for (int i = 16; i >= 1; i /= 2) {
    value += __shfl_xor_sync(mask, value, i, warpSize);
  }

  /* one thread only, for each row, updates the global sum */
  float mod = x % warpSize;
  if ((mod == 0 || mod == warpSize - 1) && r != warpSize*warpSize - 1) {    
    x += blockIdx.x*warpSize;
    y += blockIdx.y*warpSize;
    atomicAdd(r + (x + y)*incr, value);
  }
}

It can be launched with, for example:

void add_enumerate(const int m, const int n, const float* p,
    const int incp, const float* q, const int incq, float* r,
    const int incr) {
  cudaMemset(r, 0, (m + n - 1)*sizeof(float));
  dim3 block(warpSize, warpSize);
  dim3 grid((m + warpSize - 1)/warpSize, (n + warpSize - 1)/warpSize);
  kernel_add_enumerate<<<grid,block>>>(m, n, p, incp, q, incq, r, incr);
}

Further work may include:

It may be beneficial to work with log-probabilities rather than probabilities.
At the end of the kernel, atomicAdd is used to reduce across blocks. Other reduction approaches might be used.
The approach generalizes to discrete random variables with support on any contiguous range of integers by tracking the lower bound separately. If $l_x$ and $l_y$ are the lower bounds of $x$ and $y$ , then $l_{x+y} = l_x + l_y$ is the lower bound of $x + y$ .